Introducing the Unit 3 Parent Functions and Transformations Answer Key, an invaluable resource that empowers students to conquer the complexities of function transformations. This comprehensive guide unveils the secrets behind parent functions, illuminating their significance in shaping and manipulating mathematical landscapes.
Delve into the intricacies of transformations, unraveling their types and effects on parent functions. Witness how translations, reflections, and rotations alter the very fabric of functions, while scaling and stretching reshape their contours. Explore the art of combining transformations, mastering the order of operations to achieve desired outcomes.
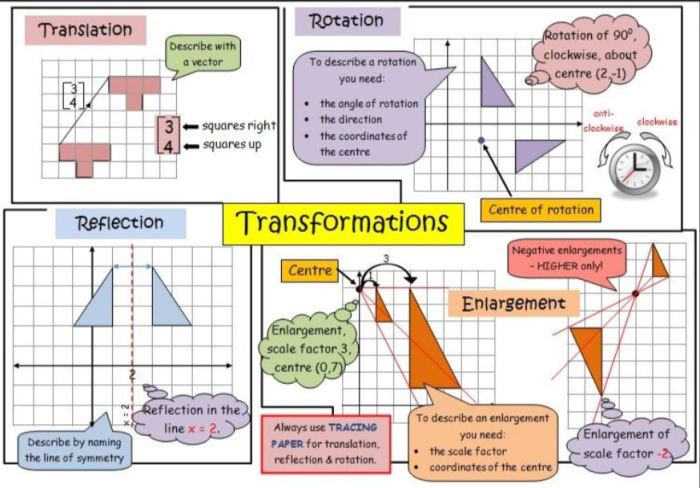
Parent Functions
Parent functions are fundamental functions that serve as building blocks for more complex functions. They provide a basis for understanding the behavior of transformations and how they affect the shape and position of graphs.
Common parent functions include linear functions (y = mx + b), quadratic functions (y = ax² + bx + c), exponential functions (y = a^x), and logarithmic functions (y = log ax). Each parent function has a unique shape and set of characteristics.
Parent functions play a crucial role in transformations because they allow us to understand the effects of translations, reflections, and rotations on the shape and position of graphs. By applying transformations to parent functions, we can create new functions with different properties.
Transformations
Transformations are mathematical operations that alter the position, shape, or size of a function’s graph. There are three main types of transformations: translations, reflections, and rotations.
- Translationsshift the graph of a function horizontally or vertically without changing its shape.
- Reflectionsflip the graph of a function over a horizontal or vertical line, creating a mirror image.
- Rotationsturn the graph of a function around a fixed point, changing its orientation.
Transformations can be applied to any function, including parent functions. By combining different transformations, we can create new functions with a wide range of shapes and properties.
Combining Transformations
Transformations can be combined to create more complex transformations. When combining transformations, it is important to apply them in the correct order. The order of operations for combining transformations is:
- Translations
- Reflections
- Rotations
- Scaling and stretching
By following this order, we can ensure that the transformations are applied in the correct sequence.
Applications of Transformations, Unit 3 parent functions and transformations answer key
Transformations have a wide range of applications in various fields, including:
- Physics:Transformations are used to model the motion of objects and to analyze forces.
- Engineering:Transformations are used to design and analyze structures and systems.
- Design:Transformations are used to create patterns, shapes, and images.
By understanding how transformations work, we can use them to model real-world phenomena and to create new and innovative designs.
Parent Function Library
| Function | Equation | Graph | Key Characteristics |
|---|---|---|---|
| Linear | y = mx + b | Straight line | Slope (m) and y-intercept (b) |
| Quadratic | y = ax² + bx + c | Parabola | Vertex (h, k) and axis of symmetry (x = h) |
| Exponential | y = a^x | Exponential curve | Base (a) and initial value (y-intercept) |
| Logarithmic | y = logax | Logarithmic curve | Base (a) and domain (x > 0) |
The parent function library provides a quick reference for the most common parent functions, their equations, graphs, and key characteristics. This library can be used to understand the effects of transformations on different types of functions.
Practice Problems
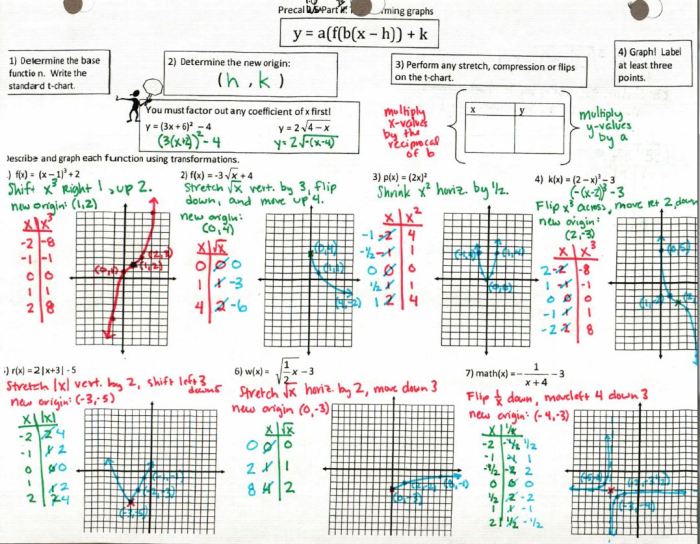
Practice problems involving transformations of parent functions can help you to understand the concepts and apply them to real-world situations. Here is an example of a practice problem:
Problem:Graph the function y = (x – 2)² + 3.
Solution:
- Identify the parent function (y = x²)
- Apply the translation (h = 2, k = 3): (x
2)² + 3
- Graph the transformed function
By following these steps, we can graph the transformed function and understand how the translation affects its shape and position.
Popular Questions: Unit 3 Parent Functions And Transformations Answer Key
What is the purpose of a parent function?
Parent functions serve as the foundation for transformations, providing a starting point for manipulating and creating new functions.
How do transformations affect the graph of a parent function?
Transformations shift, flip, rotate, stretch, or shrink the graph of a parent function, altering its shape and position.
Can transformations be combined?
Yes, multiple transformations can be combined to create complex function transformations.
What is the order of operations for combining transformations?
The order of operations for combining transformations is: translations, reflections, rotations, scaling, and stretching.
How can transformations be used in real-world applications?
Transformations find applications in physics (modeling motion), engineering (designing structures), and computer graphics (creating animations).